

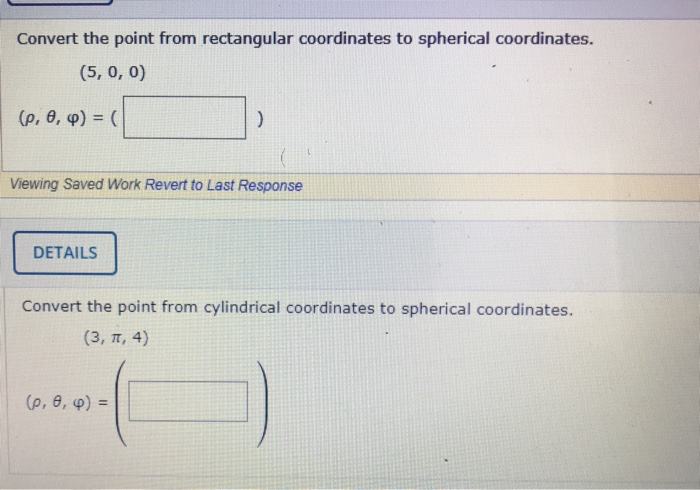
After entering the values to be converted, either click on the calculator or confirm with the Enter key. ) T ransformation coordinates Spherical (r,) Cartesian (x,y,z) x rsincos y rsinsin z rcos T r a n s f o r m a t i o n c o o r d i n a t e s S p h e r i c a l ( r,, ) C a r t e s i a n ( x, y, z) x r sin cos y r sin sin z r cos. The valid values for the respective system can be found by moving the mouse over the input examples. This works in all directions and with all valid values. Positive semi-axis z and radius from the. Here you can convert the most common coordinates into the other formats. Converts from Cartesian (x,y,z) to Spherical (r,) coordinates in. Radius - is a distance between coordinate system origin and the point. ,y y or, in other words, there is a y such. Azimuth angle is the same as the azimuth angle in the cylindrical coordinate system. Geometry Honors Geometry online textbook: use classlink app or Probability Coordinate Geometry Thursday, 8/11: Review Friday, 8/12: Multiple Choice. Let ( 1, 1, 1 ) ⇒ x = 1, y = 1, z = 1 Convert from rectangular to spherical coordinates ρ = x 2 + y 2 + z 2 , θ = tan − 1 ( x y ), ϕ = cos − 1 ( ρ z ) Therefore, ρ = ( 1 ) 2 + ( 1 ) 2 + ( 1 ) 2 ⇒ ρ = 3 θ = tan − 1 ( 1 1 ) ⇒ θ = 4 π ϕ = cos − 1 ( 3 1 ) ⇒ ϕ = 0.955 Spherical coordinates ( 3 , 4 π , 0.Since virtually everything we do in this course deals with three dimensional space, it makes sense to start with a short discussion of how to represent a point in 3-D space. This system defines a point in 3d space with 3 real values - radius, azimuth angle, and polar angle. installation described demand suite vegas square chris attention advance. Spherical coordinates are depicted by 3 values, (r,, ). We use the sine and cosine functions to find the vertical and horizontal. here business who web also now help m re get pm view online first am been. This cartesian (rectangular) coordinates converter/calculator converts the spherical coordinates of a unit to its equivalent value in cartesian (rectangular) coordinates, according to the formulas shown above. Although, the math involves the simple trigonometric functions and the. Let ( 1, 1, 1 ) ⇒ x = 1, y = 1, z = 1 Convert from rectangular to spherical coordinates ρ = x 2 + y 2 + z 2, θ = tan − 1 ( y x ), ϕ = cos − 1 ( z ρ ) Therefore, ρ = ( 1 ) 2 + ( 1 ) 2 + ( 1 ) 2 ⇒ ρ = 3 θ = tan − 1 ( 1 1 ) ⇒ θ = π 4 ϕ = cos − 1 ( 1 3 ) ⇒ ϕ = 0.955 Spherical coordinates ( 3, π 4, 0.955 ) \begin \right) \\ Spherical coordinates have the form (,, ), where, is the distance from the origin to the point, is the angle in the xy plane with respect to the x-axis and is the angle with respect to the z-axis.These coordinates can be transformed to Cartesian coordinates using right triangles and trigonometry. As for how to convert between the two, theres really no way to do it without math. When we know a point in Cartesian Coordinates (x,y) and we want it in Polar Coordinates (r,) we solve a right triangle.


 0 kommentar(er)
0 kommentar(er)
